Graph clustering is an important unsupervised learning technique for partitioning graphs with attributes and detecting communities. However, current methods struggle to accurately capture true community structures and intra-cluster relations, be computationally efficient, and identify smaller communities.
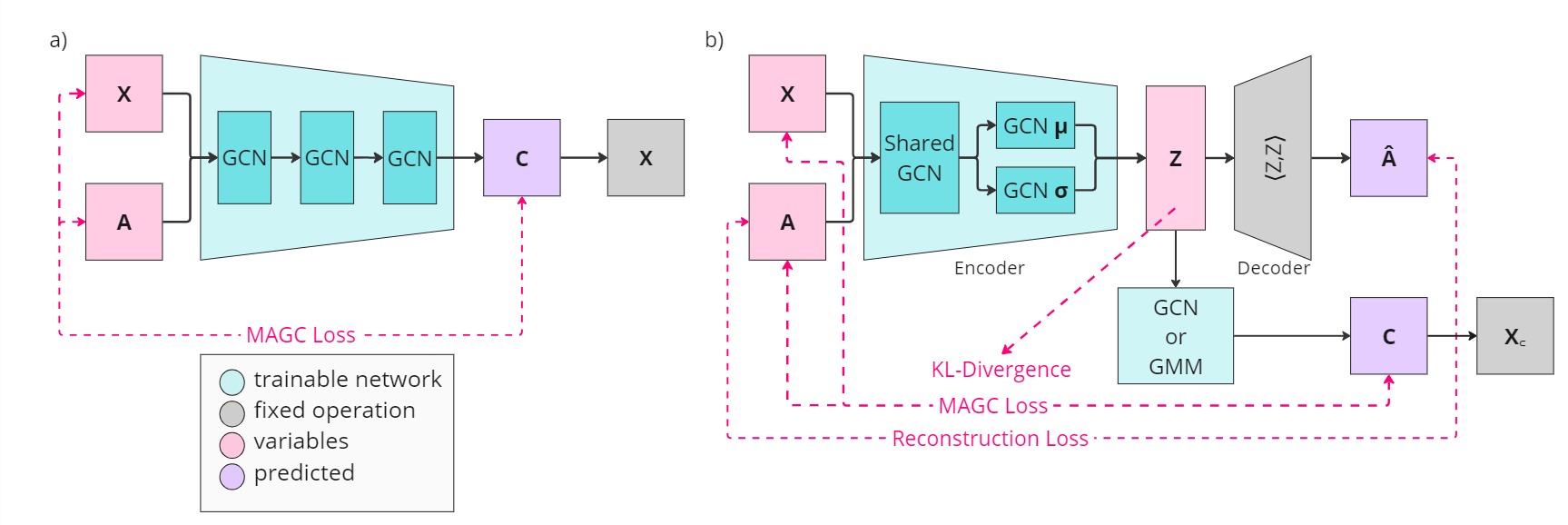
We address these challenges by integrating coarsening and modularity maximization, effectively leveraging both adjacency and node features to enhance clustering accuracy. We propose a loss function incorporating log-determinant, smoothness, and modularity components using a block majorization-minimization technique, resulting in superior clustering outcomes.
The method is theoretically consistent under the Degree-Corrected Stochastic Block Model (DC-SBM), ensuring asymptotic error-free performance and complete label recovery. Our provably convergent and time-efficient algorithm seamlessly integrates with graph neural networks (GNNs) and variational graph autoencoders (VGAEs) to learn enhanced node features and deliver exceptional clustering performance. Extensive experiments on benchmark datasets demonstrate its superiority over existing state-of-the-art methods for both attributed and non-attributed graphs.
$$ \begin{align*} \mathcal{L}_{\text{MAGC}} =& \quad \textrm{tr}(\tilde{X}^TC^T\Theta C\tilde{X}) + \frac{\alpha}{2}\|C\tilde{X} -X\|_F^2 \\ &- \frac{\beta}{2e}\textrm{tr}(C^TBC) - \gamma \log\det(C^T\Theta C + J) \end{align*} $$